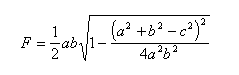
Sommer und Herbst 96 verbrachte ich segelnderweise in der Aigais. Kurz vor Törnbeginn entdeckte ich ein defektes Vorsegel. Zum Glück gibt es im Lagerschuppen dutzende Segelsäcke mit Reservesegeln. Zum Glück! Dachte ich...
Hast Du schon mal versucht, einem Segelsack anzusehen, welchen Inhalt er birgt? Da gibt es grosse, kleine, riesige, beschriftete und unbeschriftete Segelsäcke. Aber das hilft so gut wie nichts. Das Sack-Volumen sagt mehr über den Segelpacker aus als über die Segelgrösse. Und Aufschriften wie "Genua II" bedeuten je nach Schiffstyp etwas völlig unterschiedliches und selbst bei gleichem Schiffstyp haben die Beschrifter unterschiedliche Meinungen.
Die mühsame und zeitaufwendige Lösung: jedes Segel auspacken, vermessen und, falls nicht geeignet, wieder einpacken.
Am einfachsten zu messen ist die Länge von Vorliek, Unterliek und Achterliek. Und um bei der nächsten Suchaktion nicht wieder von vorne anfangen zu müssen, habe ich einfach eine Skizze der Segelform mit wasserfestem Filzstift auf den Segelhals gemalt und mit den Lieklängen beschriftet.
Wer es noch "seglerischer" haben will, misst auch die Senkrechte auf das Vorliek, die durch das Schothorn geht. Sie wird mit "LP" (luff-perpendicular = Vorlieks-Lot) bezeichnet. Laut IOR (International Offshore Rule) ergibt sich dann die Bezeichnung der Vorsegel einerseits aus dem Verhältnis LP / J. Dabei ist "J" die Basis des Vorsegeldreieckes, also die Länge zwischen unterer Segelbefestigung und Mast. Und andererseits aus dem Verhältnis Lieklänge zu Vorstaglänge.
|
Segel
|
LP/J
|
Vorliek
|
Fläche
|
| Genua I |
150 %
|
100 %
|
150 %
|
| Genua II |
140 %
|
95 %
|
133 %
|
| Genua III |
130 %
|
80 %
|
104 %
|
| Fock I |
100 %
|
95 %
|
96 %
|
| Fock II |
90 %
|
70 %
|
65 %
|
| Sturmfock |
60 %
|
50 %
|
30 %
|
Die Daten könnten natürlich auch auf den Segelsack geschrieben werden. Aber dann dürfte keiner mehr den Sack verwechseln...
Und bei all dem Auspacken, Messen und wieder Einpacken kam die Idee auf, doch gleich noch die Segelfläche dazuzuschreiben. Das wäre so einfach (Vorliek * LP / 2) - wenn nicht einer auf die Idee gekommen wäre, dass man doch aus den drei Kantenlängen die Fläche berechnen können müsste.
Diese Frage hat dann den ganzen Sommer lang, vor allem meine männlichen Mitsegler, beschäftigt. Besonders Mathematiker, Nautiker, Abiturienten, Architekten, Ingenieure haben sich damit manche Flautenstunden um die Ohren geschlagen, Hypothesen gebildet, Schreibtischtests durchgeführt und davon erzählt, dass das alles sicherlich in einer guten Formelsammlung zu finden wäre. Nur - wir hatten keine....
Das (vorläufige) Ergebnis: 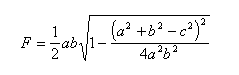
Dabei ist auf den "neumodischen" Schiffen doch alles so einfach! Man nehme eine Rollfock oder ein Rollgross und rolle nach Bedarf und Gefühl, ein und aus, wie man/frau es gerade braucht...
Egbert Weiss war mit mir auf Törn. Auch ihm hat die Frage nach der Flächenberechnung von Segeldreiecken keine Ruhe gelassen. Er hat in alten Formelsammlungen rumgestöbert und die Heronische Formel entdeckt:
| Heronische Formel: | 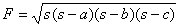 |
| wobei s = 1/2 (a + b + c), also der halbe Umfang< /td > |
gefunden in: Bartsch, Hans-Jochen: Taschenbuch mathematischer Formeln.
Verlag Harri Deutsch, Thun und Frankfurt / Main 1984
klingt ziemlich "hero(n)isch" - oder?
Ob das auch einer beweisen kann?
wieder sind zwei Jahre vergangen...
Folkert Janssen schreibt zum Segelflächen-Problem:
So schwierig ist es nicht. Aus der Schule wissen wir dass ein Dreieck durch drei Komponenten (Seitenlängen oder Winkel) vollständig bestimmt ist. Damit ist dann auch die Fäche gegeben. Im konkreten Fall liefert der Cosinus-Satz ein direkten Zugang zu den fehlenden Winkeln. Nachdem dann alles bekannt ist, kann man dann einfach die Höhe des Dreiecks bestimmen.
Der Beweis der Heronische Formel ist etwas mühsam, aber direkt aus dem Satz von Pythagoras abzuleiten. Einen viel eleganteren Beweis als meinen habe ich im Netz gefunden. Ich habe den als Text einkopiert, weil man nie weiß, wielange solche Seiten bestand haben:
Given a triangle with sides a,b,c, semiperimeter s, and area A,
show that A^2 = s(s-a)(s-b)(s-c).
Solution: Drop an altitude (of length h) to the side of length c.
Then A = (1/2)ch, so A^2 = c^2 h^2 / 4.
Use the Pythagorean Theorem to obtain the following system:
(1) x^2 + h^2 = a^2
(2) y^2 + h^2 = b^2
(3) x + y = c
Substitute y = c - x into (2) and simplify.
Then subtract the result from (1).
You will find that
2cx = a^2 - b^2 + c^2.
From (1),
4c^2 h^2 = 4a^2 c^2 - 4c^2 x^2
= (2ac + 2cx) (2ac - 2cx)
= (2ac + a^2 - b^2 + c^2)(2ac - a^2 + b^2 -c^2)
From (1),
4c^2 h^2 = 4a^2 c^2 - 4c^2 x^2
= (2ac + 2cx) (2ac - 2cx)
= (2ac + a^2 - b^2 + c^2)(2ac - a^2 + b^2 -c^2)
= ((a+c)^2 - b^2) (b^2 - (a-c)^2)
= (a+c+b)(a+c-b)(b+a-c)(b-a+c)
= (2s)(2s-2b)(2s-2c)(2s-2a)
= 16s(s-a)(s-b)(s-c)
Soviel zum Beweis der Heronischen Formel.
Aber vielleicht gibts ja doch noch eine Möglichkeit mit dem Sinus oder wenigstens mit dem Cosinus oder vielleicht sogar mit dem Semiversus ...?
Markus Bärlocher
| © Markus Bärlocher | Tel: | (+49) 9155-1715 |
Zurück |
| Schulstr. 23 | Web: | www.lau-net.de/baerlocher | |
| D-91245 Hüttenbach |  |